Хмельник Соломон Ицкович. Обтекание тела в трубе

Хмельник С. И.

Обтекание тела в трубе

Новый метод и MATLAB-программа

Аннотация

В [1] предложен вариационный принцип экстремума для вязкой несжимаемой и сжимаемой жидкости, из которого следует, что уравнения Навье-Стокса являются условиями единственного экстремума некоторого функционала. Предлагается также метод поиска этого экстремума, который является одновременно и методом решенгия этих уравнений.

Здесь описывается основанная на этом методе программа расчета обтекания тела в трубе - вычисления скорости и давления жидкости во всех точках трубы.

Содержание

1. Описание метода

2. Постановка задачи

3. Основная программа

4. Расчет

5. Отображение

Литература

Программы

1. Описание метода

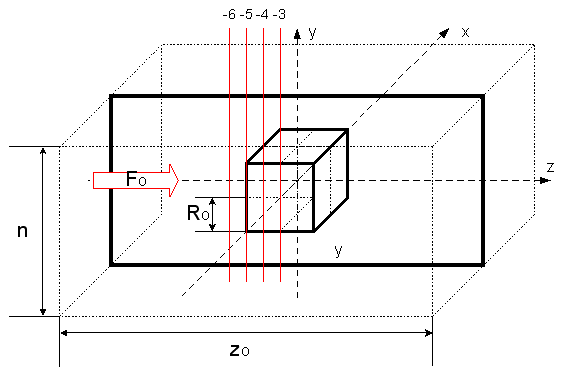
0x01 graphic

Прелагаемый метод распространяется и на тот случай, когда в труба имеет произвольную конфигурацию, и в ней находится некоторое обтекаемое тело.

В программной реализации метода используютсяоперации с интегралами по объему потока жидкости. Этот объем представляется объемной сеткой. Точка-узел сетки имеет значение 1, если эта точка доступна потоку жидкости, и - 0, если точка принадлежит стенке или препятствию на пути потока. Задание области существования потока - единственное, что требуется для описания задачи. Не требуется указания граничных условий - они вычисляются в процессе решения.

2. Постановка задачи

Здесь мы рассмотрим течение в бесконечно длинной трубе произвольной конфигурации. Выделим в такой трубе некоторый отрезок и будем полагать, что форма сечения и скорости на обоих торцах этого отрезка совпадают. Тогда вместо этого отрезка можно рассмотреть эквивалентную ему систему в виде такого отрезка, торцы которого соприкасаются так, что поток жидкости из левого (например) торца втекает непосредственно в правый торец. Очевидно, течение в любом отрезке бесконечно длинной трубы совпадает с течением в построенной системе.

Надо отметить, что точность расчетов увеличивается с увеличением длины рассчитываемого отрезка, поскольку с увеличением расстояния торца отрезка от заслонки зависимость распределения скоростей на торцах от длины отрезка уменьшается, а сами распределения на торцах становятся одинаковыми - именно такое допущение делается при решении задачи.

Здесь мы рассмотрим течение в бесконечно длинной трубе квадратного сечения со стороной n, в которой находится абсолютно твердый куб с полустороной Ro. Рассмотрим "закольцованный" отрезок трубы длиной Zo, где действуют постоянные массовые силы Fo, определяемые по (5) и направленные вдоль оси трубы oz - см. фиг. 1. Пусть еще сечение трубы определено в координатах (x,y) и является квадратом с полустороной n.

На фиг. 1 проведены вертикали (-6,-5,-4,-3), которые проходят через центры сечений, отстоящих на (-6,-5,-4,-3) от центра куба. Эти обозначения понадобятся в дальнейшем.

0x01 graphic

Фиг. 1.

Отметим, что программа с минимальными изменениями может быть использована при другой конфигурации трубы и\или обтекаемого тела. Обтекаемое тело может отсутствовать вовсе. Тогда по этой программе можно расчитывать распределение скоростей по сечению трубы произвольной конфигурации. В частном случае для трубы с круглым сечением определяется известное распределение Пуазеля.

3. Основная программа

М-функция для расчета имеет вид:

function [vx,vy,vz,Ez,Py,Pz,Gz,Dz,...

Pzmid,Gzmid,Dzmid,PPP,n,zz,ro]...

=testDawleModif8

В программе задаются следующие определенные выше величины:

n, zz=zo, Ro, Fo, mu, ro, а также

Q - область существования потока,

r - некоторый коэффициент, определенный в [1] (его увеличение увеличивает точность расчета, но одновременно увеличивает и длительность расчета),

maxK - допустимое количество итераций,

maxEr - допустимая относительная ошибка нарушения второго уравнения в (1) - относительно к максимальной скорости потока.

Кроме того, задается, конечно область существования потока Q.

В результате решения определяются следующие величины:

erMin - достигнутая относительная ошибка нарушения второго уравнения в (1),

NeprMin - достигнутая относительная ошибка нарушения первого уравнения в (1),

к - достигнутое количество итераций,

Ez - область существования и величина массовых сил,

vx,vy,vz - проекции вектора скорости,

Dx, Dy, Dz - проекции вектора (2а),

Gx, Gy, Gz - проекции вектора (2в),

Px, Py, Pz - проекции скалярного давления вектора p,

Pzmid, Gzmid, Dzmid - соответственно средние значения Pz, Gz, Dz по сечению трубы,

PPP - разность давлений на торцах отрезка трубы.

Вычисляемые величины эта функция передает в рабочее пространство системы MATLAB. В дальнейшем эти величины используются функциями отображения результатов.

4. Расчет

В основной функции определяется область течения в трубе с кубическим телом на пути потока - см. фиг. 1. При этом

n=13, zo=23, Ro=5, Fo=20, mu=1, ro=1, r=39

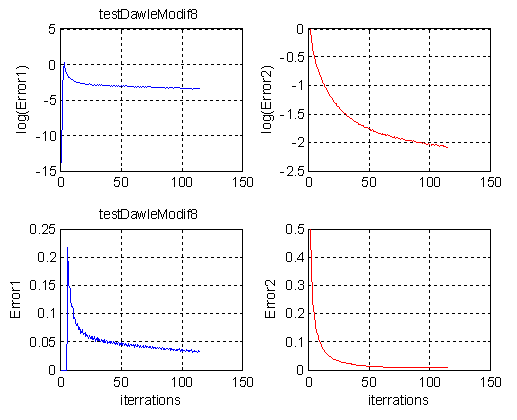
На фиг. 2 показано, как изменяются величины erMin и NeprMin при увеличении числа итераций.

0x01 graphic

Фиг. 2.

5. Отображение

Функции отображения обращаются к результатам расчета, находящимся рабочее пространство системы MATLAB.

5.1. Функция

function testDawleModif8fig1(Py,Pz,Gz,Dz,...

Pzmid,Gzmid,Dzmid,PPP,n,zz)

строит графики, показанные на фиг. 3, где показаны

-- функции Pzmid,Gzmid,Dzmid,PPP от z - см. первое окно на первой вертикали;

-- функции Pz,Gz,Dz от z при фиксированных значениях x=y=9 - см. первое окно на второй вертикали;

-- функции Pz от z при фиксированных значениях x=y=9 (верхняя кривая) и x=y=-11 (нижняя кривая) - см. второе окно на первой вертикали;

-- функции Pz от y при фиксированных значениях x=10 и z=1 (верхняя кривая) и z=19 (нижняя кривая) - см. второе окно на второй вертикали.

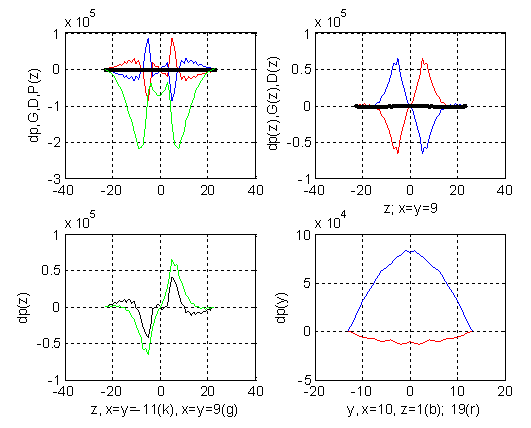
Фиг. 3.

5.2. Функция

function testDawleModif8fig2(Pz,n,zz)

строит графики, показанные на фиг. 4, где показаны функции распределения Pz(x,y) при определенном значении z.

Можно заметить следующее.

1) Квазидавление равно нулю.

2) Средний градиент давления по каждому сечению равен нулю.

3) Разность давлений, как интеграла градиента давлений, на крайних торцах отрезка трубы равна нулю.

4) Распределение градиента давления по сечению трубы и вдоль трубы неравномерно.

Фиг. 4.

5.3. Функция

function testDawleModif8fig3(Pz,Ez,n,zz)

строит графики, показанные на фиг. 5. Здесь приняты обозначения

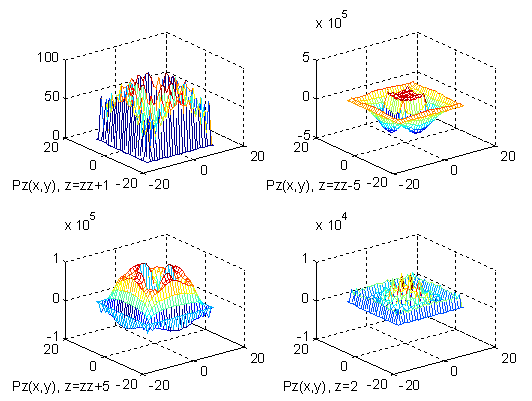
0x01 graphic

На фиг. 5 показаны

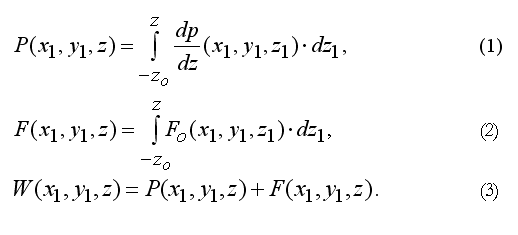
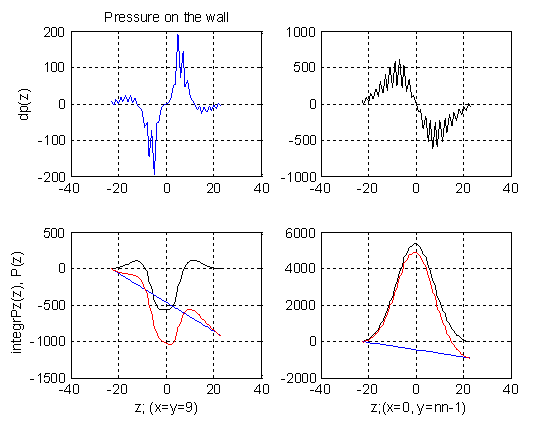
-- функция Pz от z при фиксированных значениях x=y=9 - см. первое окно на первой вертикали;

-- функция Pz от z при фиксированных значениях x=0, y=-1 - см. первое окно на второй вертикали;

-- функции (1-2) при фиксированных значениях x1=y1=9 - см. второе окно на первой вертикали;

-- функции (1-2) при фиксированных значениях x1=0, y1=nn-1 - см. второе окно на второй вертикали.

В нижних окнах графики функций (1, 2, 3) обозначены соответственно черным, синим и красным цветом.

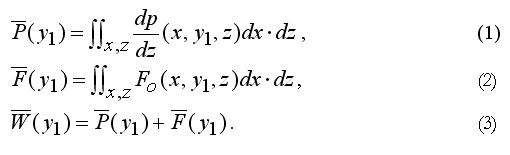
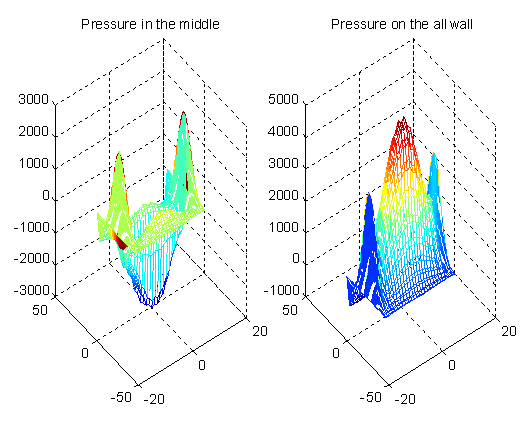
0x01 graphic

Фиг. 5.

5.4. Функция

function testDawleModif8fig4(Pz,Ez,n,zz,ro)

строит графики, показанные на фиг. 6. Здесь приняты обозначения

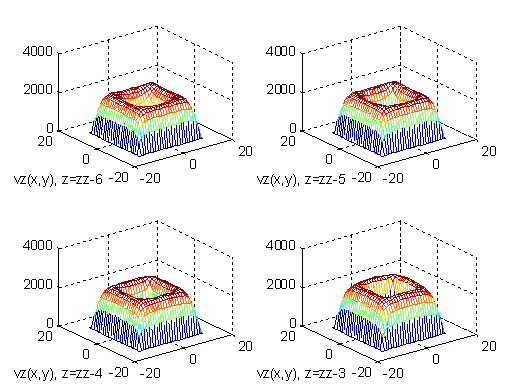
0x01 graphic

На фиг. 6 показаны функции (3)- в левом окне при y1=nn-5, в правом окне при y1=nn-1.

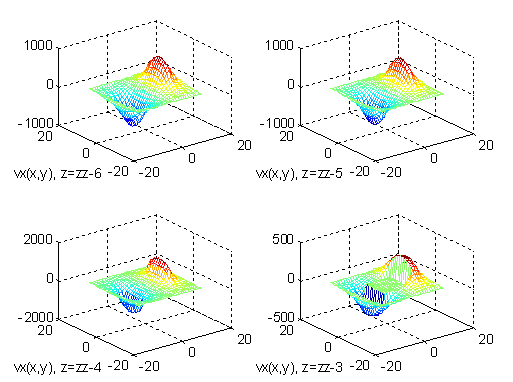
0x01 graphic

Фиг. 6.

5.5. Функция

function testDawleModif8fig5(vx,vy,vz,n,zz)

строит графики, показанные на фиг. 7.

На фиг. 1 проведены вертикали (-6,-5,-4,-3), которые проходят через центры сечений, отстоящих на (-6,-5,-4,-3) от центра куба. На фиг. 7 показаны распределения скоростей vz по этим сечениям.

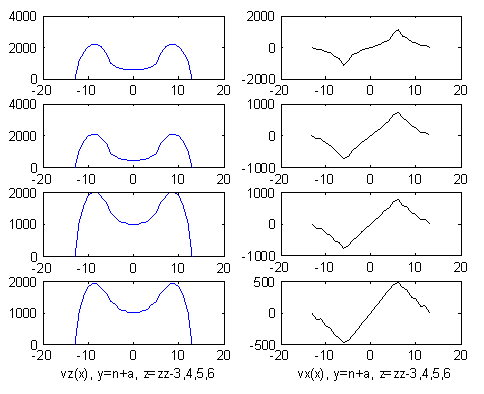
0x01 graphic

Фиг. 7.

5.6. Функция

function testDawleModif8fig6(vx,vy,vz,n,zz)

На фиг. 1 проведены вертикали (-6,-5,-4,-3), которые проходят через центры сечений, отстоящих на (-6,-5,-4,-3) от центра куба. На фиг. 8 показаны распределения скоростей vx по этим же сечениям.

0x01 graphic

Фиг. 8.

5.7. Функция

function testDawleModif8fig7(vx,vy,vz,n,zz)

На фиг. 1 проведены вертикали (-6,-5,-4,-3), которые проходят через центры сечений, отстоящих на (-6,-5,-4,-3) от центра куба. На фиг. 9 показаны распределения скоростей vz и vx по оси этих сечений при фиксированном значении y=0. Эти фигуры позволяют представить распределение скоростей при обтекании куба под действием массовых сил в бесконечно длинной трубе.

0x01 graphic

Фиг. 9.

Литература

1. Хмельник С.И. Уравнения Навье-Стокса. Существование и метод поиска глобального решения. Вторая редакция. Publisher by "MiC", printed in USA, Lulu Inc., ID 9971440, Израиль, 2011, ISBN 978-1-4583-1953-1.

Оставить комментарий © Copyright Хмельник Соломон Ицкович Размещен: 12/02/2011, изменен: 12/02/2011. 19k. Статистика. Статья: Естествознание Гидродинамика Иллюстрации/приложения: 13 шт.		Ваша оценка:
Аннотация: В книге [1] предложен новый метод решения уравнений Навье-Стокса. Эту книгу можно скачать здесь, на СИ. В этой статье описывается программа в системе MATLAB для решения указанным методом задачи обтекания тела в трубе. Открытые коды этой MATLAB-программы можно приобрести у автора на сайте http://mic34.com/bookrusmore.htm, позиция 352. С предложениями о дополнительных разработках можно обратиться по адресу [email protected].

Хмельник Соломон Ицкович : другие произведения.

Обтекание тела в трубе