?-? ?-? Т=273+150=423 К.
Находим плотность воздуха из уравнения Клапейрона,
позволяющее определять плотность газа при известных давлении и температуре,т.е.
где Рабс- абсолютное давление;
R- удельная газовая постоянная (для воздуха R=287 Дж/(кг*К));
Т- абсолютная температура.
?=748100/287*423=6,16 кг/м3.
где ?- плотность воздуха, кг/м3;
g- ускорение свободного падения, м/с2.
?=6,16*9,8=60,368-60,4 Н/м3.
Ответ: ?=6,16 кг/м3, ?=60,4 Н/м3.
Определить абсолютное и избыточное(или вакуумметрическое) давление в т.А (рис.1) и h4 , если остальные величины заданы. Налитые в резервуары жидкости с плотностями ?1 и ?2 не смешиваются и находятся в состоянии покоя. Значение давления дано в атмосферах, РА=1атм=101325 Па.
Дано:
Р1изб=0,2 атм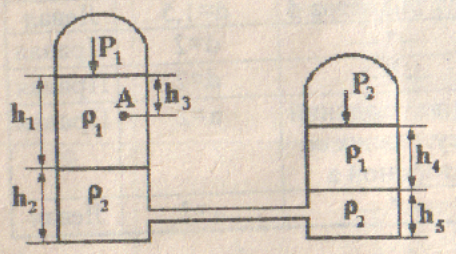
Р2вак=0,1 атм
h1=4 м
h2=3 м
h3=6 м
h5=4 м
?1=750 кг/м3
?2=900 кг/м3
------------
h4-? Рабс-?
Ризб-?
Абсолютное давление в любой точке покоящейся жидкости определяется по основному уравнению гидростатики
Где Р0- абсолютное давление на свободной поверхности жидкости;
?- плотность жидкости, кг/м3;
g- ускорение свободного падения, м/с2;
h- глубина погружения точки под свободной поверхностью, м.
В сосуде задано манометрическое Ром и вакуумметрическое Ров давления. В этих случаях перед расчетом они переводятся в абсолютное давление по формулам:
1ат - 101325 Па
0,2ат - х Па ? х=101325*0,2/1=20265 Па
1ат - 101325 Па
0,1ат - х Па ? х=101325*0,1/1=10132,5 Па
Р0изб=101325+20265=121590 Па
Р0вак=101325-10132,5=91192,5 Па
Так как в задаче рассматриваются системы с двумя сообщающими сосудами , то проведем через них плоскость равного давления 0-0
(рис.1). Найдем абсолютное давление в точке А.
Р=121590+750*9,8*4+900*9,8*6=203910 Па
Найдем избыточное давление в точке А.
Р=91192,5+750*9,8*4+900*9,8*6=173512,5 Па
Запишем выражения для абсолютного давления в двух сосудах.
Р1=Р0изб+?1gh1+?2gh3, Р2=Р0вак+?1gh4+?2gh5
Приравняв выражения между собой, определяем неизвестную величину(h4).
203910=91192,5+750*9,8*h4+900*9,8*4
203910=91192,5+7350h4+35280
203910-91192,5-35280=7350h4
Определить равнодействующую силу избыточного давления воды на плоский затвор (рис.2), перекрывающий отверстие трубы. Определить координату точки, приложения силы давления воды ZД на указанную сторону затвора.
Дано:
H1=5 м
H2=2 м
?=45®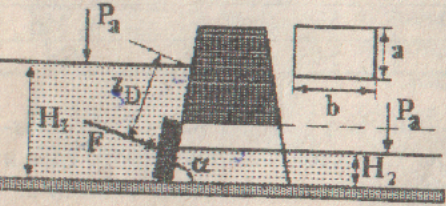
Форма сечения трубы-
-прямоугольник
а=1 м
б=1 м
сторона затвора - левая
----------------------
F-? ZД-?
Сила F избыточного давления на стенку равна произведению избыточного давления Рс в центре смоченной поверхности стенки на смоченную площадь S.
Где hс- глубина погружения центра тяжести, м;
H- толщина слоя жидкости в резервуаре, м;
Так как с другой стороны стенки также есть слой жидкости, то вычисляется сила давления жидкости со стороны этого слоя, а
результирующая сила давления определится разностью сил от первого и второго слоев.
F1=1000*9,8*(5/2)*(5/sin45)=122500
F2=1000*9.8*(2/2)*2/sin45=19600
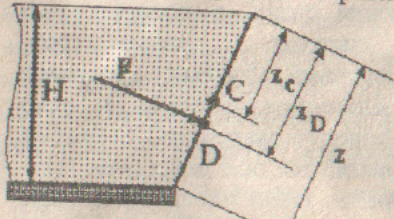
Точка Д, через которую проходит вектор силы F, называется центром давления. Давление возрастает с глубиной и имеет треугольную эпюру, поэтому центр давления D смещен в сторону наибольших давлений, то есть в общем случае находится ниже центра тяжести С . Координата ZD центра давления для стенки любой формы определяется по формуле.
Где ZC- координата центра тяжести смоченной поверхности стенки;
IC- момент инерции площади смоченной поверхности стенки относительно горизонтальной оси, проходящей через центр тяжести, м4.
Для прямоугольной стенки, верхняя кромка которой совпадает со свободной поверхностью, IC=bz3/12, S=bz, ZC=z/2. Поэтому получаем ZD=2z/3, то есть центр давления D находится от свободной поверхности на расстоянии 2z/3 в плоскости стенки или на расстоянии 2H/3 по вертикали.
Определить равнодействующую сил избыточного давления на 1 пог. м.(нормально к плоскости чертежа) поверхности АВС. Найти угол наклона, линии действия сил избыточного давления воды на поверхность АВС слева. В расчетах принять h=2 м, r=1 м.
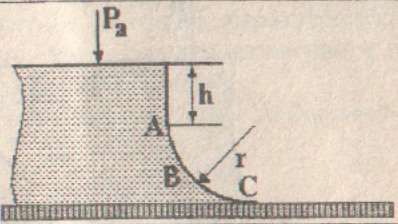
Сила F давления жидкости на криволинейную стенку, определяется геометрической суммой горизонтальной Fr и вертикальной FВ составляющих.
Горизонтальная составляющая равна силе давления на плоскую стенку, представляющую собой вертикальную проекцию А'С' криволинейной стенки.
Где Рс- давление в центре тяжести вертикальной проекции, Па;
SВ- площадь вертикальной проекции, м2;
b- длина цилиндрической стенки, м.
Вертикальная составляющая равна силе тяжести тела давления.
Где Vт.д.- объем тела давления, м3.
FВ=1000*9,8*2*3,14*12/4=15386
Так как жидкость располагается под криволинейной поверхностью, то вертикальная составляющая FВ направлена вверх. Тело давления в этом случае ограничено мнимой свободной поверхностью и называется мнимым (фиктивным), так как не заполнено жидкостью.
Линия действия равнодействующей силы давления на цилиндрические поверхности всегда направлена по радиусу и проходит через их геометрическую ось О (рис.3). Угол наклона вектора этой силы к горизонту вычисляем по формуле:
?=arctg(15386/9800)=arctg1.57=57.51-58®
1



