Жила В.А.
Сокращение времени при переменной скорости света.
- --
скорость света не зависит от скорости источника света.
- -- скорость света в данный момент времени в данной точке пространства есть максимальная скорость, возможная в природе.
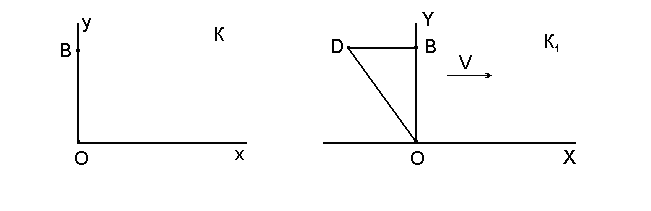
|
|
||
Выведена формула, аналогичная формуле Лоренца сокращения времени, при переменной скорости света. | ||
Жила В.А.
Сокращение времени при переменной скорости света.

|