![]()
![]()
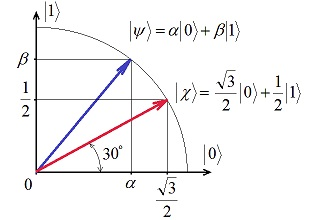
(1)
![]()
![]()
![]()
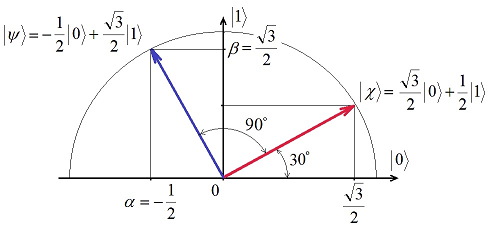
![]()
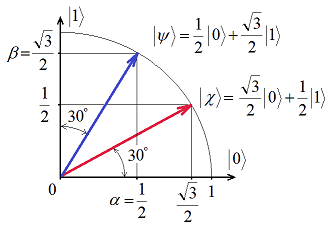
,
![]()
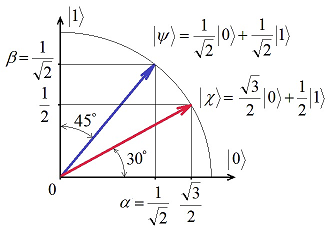
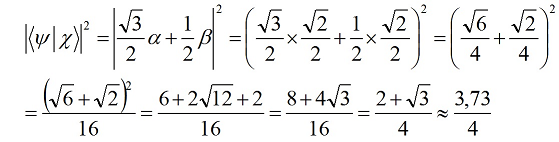
![]()
![]()
![]()
![]()
01.11.2013
The task of quantum computing
Putenikhin P.V.
|
|
||
Рассмотрена в учебных целях задача по измерению поляризованных фотонных потоков с различной поляризацией с помощью одного и того же поляризатора. Вычисления вероятности прохождения этих фотонов произведены с использованием проективной математики квантовых вычислений | ||
![]()
![]()
(1)
![]()

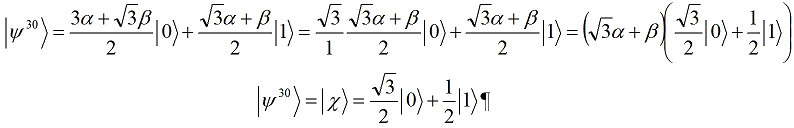
![]()

![]()

![]()

,
![]()

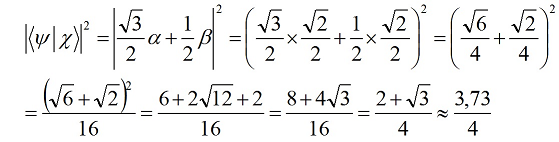

![]()

![]()

![]()
![]()
01.11.2013
The task of quantum computing
Putenikhin P.V.
|